¿Sabías que las desigualdades matemáticas se utilizan frecuentemente dentro del área profesional? Si tus conocimientos sobre álgebra están un poco oxidados, ¡no te preocupes! Esta nota te ayudará a recordar los conocimientos básicos necesarios para entender este tipo de operaciones.
Las desigualdades matemáticas se utilizan para expresar la relación que existe entre dos valores distintos. Muchas veces, este tipo de expresiones pueden contener valores incógnitos, lo que las convierte en una inecuación que debe resolverse mediante un procedimiento matemático.
En el siguiente artículo te enseñaremos qué son las desigualdades matemáticas, cómo se resuelven las operaciones con estas expresiones y de qué manera se utilizan dentro del área laboral. ¡Es momento de empezar a tomar nota!
¿Qué son las desigualdades matemáticas?
Como su mismo nombre lo dice, las desigualdades matemáticas se utilizan para expresar el tipo de relación que existe entre dos expresiones algebráicas que contienen valores distintos.
En ese sentido, una desigualdad matemática denota la relación de orden que existe entre los dos valores a través de una serie de signos que indican el mayor, menor, mayor igual o menor igual.
Dependiendo del tipo de desigualdad matemática que se manifieste, se tendrá que llevar a cabo una operación matemática diferente.
Signos de desigualdad matemática
Para poder entender mejor cómo es que se es que se expresan los diferentes tipos de relación que hay entre las variables, a continuación te indicaremos cuáles son los signos de las desigualdades matemáticas:
- a ≠ b : indica que a no es igual a b
- a < b : indica que a es menor que b
- a > b : indica que a es mayor que b
- a ≤ b : indica que a es menor o igual que b
- a ≥ b : indica que a es mayor o igual que b
¿Las inecuaciones y desigualdades matemáticas son lo mismo?
Si bien estos conceptos a veces suelen ser confundidos o se utilizan para expresar una misma proposición, la realidad es que hay una clara diferencia entre desigualdad matemática e inecuación.
Por un lado, las inecuaciones suelen expresar una desigualdad cuyo resultado puede ser incongruente o, simplemente, no tener solución alguna. En el caso de una desigualdad matemática, esta puede no tener incógnita.
Por ejemplo, en la siguiente expresión: 4 < 7, podemos decir que es un ejemplo de desigualdad matemática pero no de una inecuación, ya que no existe ningún valor desconocido.
En ese sentido, podemos afirmar que una inecuación puede ser una desigualdad, más una desigualdad matemática no tiene que ser necesariamente una inecuación. Por lo tanto, afirmar que ambos conceptos son lo mismo es un error.
 Fuente: Pixabay
Fuente: Pixabay
¿Cuáles son los tipos de desigualdades matemáticas?
De acuerdo a la página de la empresa Delsol, negocio que ofrece softwares de contabilidad a empresas, se pueden distinguir 2 tipos de desigualdades matemáticas según su nivel de aceptación: las desigualdades estrictas y las desigualdades amplias o no estrictas.
Desigualdades estrictas
Una desigualdad estricta se produce cuando ambos valores son diferentes y, por lo tanto, uno es mayor que el otro. En ese sentido, podemos encontrar dos tipos de relaciones:
- La notación a < b que significa que a es menor que b.
- La notación a > b que significa que a es mayor que b.
Si bien el símbolo ≠ también se utiliza para señalar a dos valores diferentes, no se considera dentro de las desigualdades estrictas, ya que no precisa que un valor sea mayor que otro.
Desigualdades amplias o no estrictas
Una desigualdad no estricta, o amplia, es aquella en donde no se puede determinar si uno de los valores es mayor, menor o igual que el otro. Aquí podemos encontrar los siguientes tipos de relaciones:
- La notación a ≤ b, que significa que a es menor o igual que b.
- La notación a ≥ b, que significa que a es mayor o igual que b.
 Fuente: Pixabay
Fuente: Pixabay
¿Cuáles son las propiedades de las desigualdades matemáticas?
Hay una serie de reglas de las desigualdades matemáticas que sirven para resolver operaciones con estas expresiones algebráicas. De acuerdo al canal de YouTube, Math2me, se puede explicar cada una de ellas de la siguiente manera:
1. Regla de adición y sustracción
Cuando a ambas partes de una expresión se les suma o resta una misma cantidad, el sentido de la desigualdad numérica no varía. Es decir, que el signo se mantiene. Por ejemplo:
8 > 5
8 (+ 3) > 5 (+ 3)
11 > 8
8 (- 2) > 5 (- 2)
6 > 4
2. Regla de multiplicación y división por número positivo
A partir de una desigualdad matemática establecida, si se divide o se multiplica por el mismo número positivo, el sentido de la desigualdad se conserva. Por ejemplo:
25 > 10
25 (×3) > 10 (×3)
75 > 30
25 (÷5) > 10 (÷5)
5 > 2
3. Regla de multiplicación y división por número negativo
Cuando a las diferentes partes de una desigualdad establecida se les multiplica o divide por un mismo número en negativo, el sentido de la desigualdad matemática cambia. Por ejemplo:
25 > 10
25 × (-2) < 10 × (-2)
-50 < -20
25 ÷ (-5) < 10 ÷ (-5)
-5 < -2
Nota: Recuerda que, en caso de las variables negativas, mientras más cercano esté el número al 0, es mayor.
4. Regla de transitividad
En las desigualdades matemáticas, cuando se tiene una expresión equivalente a una de las partes, entonces se puede sustituir por la misma y conservar la desigualdad. Por ejemplo:
6 > 3
6 = 1 + 2 + 3
1 + 2 + 3 > 3
5. Regla del recíproco
Si en las desigualdades matemáticas, ambos números tienen el mismo signo, es decir, que ambos son positivos o negativos, al aplicarles el recíproco también se modifica el sentido de la desigualdad. Por ejemplo:
5 > 3
⅕ < ⅓
0.2 < 0. 33
-3 < -2
- ⅓ > - ½
- 0.33 > - 0.5
6. Regla de la función monótona
Considerando que ambos números de una desigualdad matemática son positivos, cuando se aplica una función monótona creciente a ambos lados, el sentido de la desigualdad se conserva. Por ejemplo:
3 < 5
3² < 5²
9 < 25
 Fuente: Pexels
Fuente: Pexels
Ejercicios de desigualdades matemáticas
Ahora, llegó el momento de aprender cómo resolver ejercicios de desigualdades matemáticas paso a paso. Si bien este puede llegar a ser un tema un poco complejo, te presentaremos una serie de ejercicios básicos que te ayudarán a entender cómo realizar operaciones con desigualdades ante la ausencia de un valor.
A continuación, te mostraremos una serie de ejemplos de desigualdades lineales que son las más utilizadas:
Ejemplo 1: 6x-10>3x+5
Paso 1: Trasladar los términos semejantes hacia lados diferentes.
6x-3x > 5+10
Paso 2: Despejar x.
3x > 15
x > 15/3
x > 5
El conjunto solución es: {5; ∞}
La representación gráfica sería:

Fuente: Ejercicios de álgebra de Pearson
Ejemplo 2: 2x-6+3x ≥ 8x+21
Paso 1: Trasladar los términos semejantes hacia lados diferentes.
2x+3x-8x ≥ 21+6
Paso 2: Simplificar los términos.
-3x ≥ 27
x ≤ 27/-3
x ≤ -9
El conjunto solución es: {-∞; 9]
La representación gráfica sería:
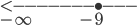
Fuente: Ejercicios de álgebra de Pearson
Ejemplo 3: 2(x+1) - 3(x-2) < x + 6
Paso 1: Resolver lo que está en paréntesis
2x + 2 - 3x + 6 < x + 6
Paso 2: Trasladar los términos semejantes hacia lados diferentes.
2 + 6 - 6 < x - 2x + 3x
Paso 3: Despejar x.
2 < 2x
1 < x
El conjunto solución es: (1, ∞)
La representación gráfica sería:

Fuente: Superprof
¿Cómo se usan las desigualdades matemáticas dentro del ámbito laboral?
La importancia de las desigualdades matemáticas se basa en el uso que se les da tanto en el trabajo que desempeñan algunos profesionales, como en algunas situaciones de la vida cotidiana.
Cuando se habla del uso de las desigualdades matemáticas, se hace referencia a las situaciones en donde se establecen una serie de límites. Como por ejemplo, el límite de velocidad, el límite de minutos para realizar llamadas o el tiempo aproximado que te toma ir de la casa al trabajo.
A continuación, te mencionaremos algunas profesiones en las cuales resulta útil tener conocimientos de desigualdad matemática:
1. Programador
Los programadores informáticos deben saber cómo aplicar las desigualdades matemáticas para el desarrollo de aplicaciones, páginas web y configuraciones de seguridad. Este tipo de operaciones pueden ser de utilidad para resolver problemas, como por ejemplo: el tiempo aproximado que se necesita para actualizar una base de datos.
2. Administrador de empresas
Los gerentes del área empresarial hacen uso de las desigualdades matemáticas para hacer mediciones estadísticas, realizar compras, evaluar los aumentos, entre otras funciones. Además, también se pueden usar en el área de la publicidad y marketing digital, como para planificar el presupuesto de una campaña utilizando las desigualdades basadas en el costo por clic.
3. Analista financiero
Algunos cargos, como los de contadores, auditores, analistas de presupuesto o aseguradores, hacen uso de las desigualdades matemáticas para equilibrar las cuentas, fijar un estimado de precios y establecer presupuestos.
También se puede aplicar la desigualdad matemática dentro del proceso de planificación financiera personal. De acuerdo a Elain King, docente del curso online de Finanzas personales, es importante que una persona pueda tener un presupuesto que esté alineado a sus metas, valores y que tenga un fondo de ahorro específico y medible en el tiempo.
4. Ingeniero
El campo de la ingeniería es uno de los que más requiere conocimientos algebráicos, incluyendo el tema de las desigualdades matemáticas. Aquí podemos encontrar distintos profesionales de la ingeniería, como bioquímicos, químicos, eléctricos, mecánicos y nucleares. Ellos aplican este conocimiento para realizar cálculos y medir los componentes sólidos y líquidos que utilizan en sus labores con la mayor precisión posible.
5. Arquitectos y constructores
Otra forma de saber cómo usar las desigualdades matemáticas, se puede encontrar dentro del campo de la construcción civil, al momento de tener que medir y calcular el uso estimado de diferentes recursos que se emplearán a lo largo del proyecto que se está ejecutando.
6. Personal sanitario
Las desigualdades matemáticas también son muy utilizadas dentro del área de salud. Por ejemplo, cuando los doctores o enfermeros necesitan calcular la dosis correcta de un medicamento que los pacientes deben consumir en función a su peso. Esto es necesario para evitar que haya una sobredosis que ponga en riesgo la vida del paciente.
 Fuente: Pexels
Fuente: Pexels
Esperamos que esta nota te haya ayudado a comprender que es una desigualdad matemática y cómo puedes aplicarla en tu rutina diaria. Recuerda que las matemáticas son una herramienta importante que nos ayuda a la resolución de problemas. Además, al practicarlas con frecuencia, lograrás desarrollar tu pensamiento abstracto aún más.
Si quieres conocer más herramientas que puedan ayudarte a gestionar tu empresa, entonces no te olvides de visitar nuestro catálogo de cursos online sobre Emprendimiento y negocios que te ayudarán a triunfar dentro del rubro empresarial. ¡Nos vemos en la siguiente nota!