Saber cómo calcular el intervalo de confianza es esencial para la actividad económica de tu empresa, ya que te será de gran utilidad para llevar las finanzas de tu negocio de forma tal que puedas desarrollar las estrategias adecuadas para que tu organización siga creciendo.
Constantemente, estamos realizando mediciones y estudiando análisis estadísticos de manera automática, sin que sea esto una actividad formal. Sin embargo, existen casos en los que una medición adecuada se convierte en un recurso muy importante, y es necesario establecer su precisión, ya que de ella dependerá la toma de decisiones importantes. ¿Y qué tiene que ver esto con el intervalo de confianza? Mucho, y lo verás a continuación.
Calcular el intervalo de confianza es necesario para conocer la precisión de una medición, lo que resulta muy importante para la validación de datos e información recabada y permite conocer cuán estable es un valor aproximado.
Pero… ¿Qué es un intervalo de confianza y para qué sirve exactamente? ¿Cuáles son los aportes que puede significar el intervalo de confianza en los procesos de mi empresa? ¡Acompáñanos a descubrirlo!
¿Qué es un intervalo de confianza?
Gabriel Mendoza, profesor del curso online de Fundamentos estadísticos para el análisis de datos, define a un intervalo de confianza como “un rango de valor que se determina en base a la información muestral, en la cual es probable que el parámetro poblacional esté contenido”.
El intervalo de confianza es una técnica de estimación muy importante en el campo de la estadística inferencial: se trata de un par o de varios pares de números entre los cuales se estimará que estará cierto valor desconocido, respecto de un parámetro poblacional, con un determinado nivel de confianza.
Este par de números del que hablamos, determina un intervalo, el cual se calcula a través de datos que provienen de una muestra, y el valor desconocido es un parámetro poblacional. De eso se trata un intervalo de confianza.
Básicamente, el intervalo de confianza corresponde a un rango de valores, que cuenta con una distribución normal y en el cual se encuentra (de forma altamente probable) el valor real de una variable concreta.
Ahora que ya sabemos qué es precisamente el intervalo de confianza, vayamos a otro punto muy importante: ¿para qué sirve calcular el intervalo de confianza?
¿Para qué sirve un intervalo de confianza?
Los intervalos de confianza son una herramienta esencial en las empresas porque sirven para el control estadístico de los procedimientos, siendo una técnica que se aplica en diferentes procesos como la producción y venta de bienes o servicios. Dentro de una posibilidad estimada, calcular un intervalo de confianza permite acotar uno o varios valores, entre los cuales se encuentra la estimación puntual que se indaga.
Llevar un buen control estadístico, a su vez, permite tener conocimiento del intervalo que existe en cada uno de los procesos que se quieran analizar; por lo tanto, calcular el intervalo de confianza te permitirá determinar el verdadero valor de un parámetro.
Esencialmente, la estimación del intervalo de confianza puede asegurarte una credibilidad estadística. Según la información del Banco Confinandina "un intervalo de confianza en estadística permite expresar con precisión si la estimación de la muestra coincide con el valor de toda la población".
Según menciona el portal especializado, la razón por la cual se le da tanta importancia a la estimación por intervalos por encima de la estimación puntual es porque esta última no ofrece información sobre algún error de estimación.
Elementos del intervalo de confianza
Una vez que conoces qué es el intervalo de confianza y su importancia al momento de hacer ciertos estudios y análisis, es la hora en la que tienes que comprender todos los componentes que conforman este tipo de recurso.
Antes de pasar a la fórmula de un intervalo de confianza, debes tener en claro cuáles son los componentes que forman parte de un intervalo de confianza para la media.
Considera estos tres elementos al momento de calcular tu intervalo de confianza:
-
El tamaño de la selección de la muestra: este elemento tiene que ver con la proporción de datos que se utilice para el valor muestral. Lo importante de este punto es determinar si el tamaño de la selección de la muestra se acerca, más o menos, al valor muestral.
-
El nivel de confianza: es lo que nos informa acerca del porcentaje del nivel de certeza de nuestra estimación. Generalmente, los niveles de confianza varían entre un 95% y 99%.
-
El margen de error de la estimación: en el cálculo del intervalo de confianza, este elemento se nombra como alfa, y marca la posibilidad que tiene el valor poblacional de estar fuera del intervalo.
-
Estimación de la muestra: este factor se relaciona con los valores de la media, la varianza, las diferencias de la media, entre otros. Es en esos valores en los que se fundamenta el cálculo del intervalo.
Estos son algunos de los elementos que conforman el intervalo de confianza. Sin embargo, existen una serie de requisitos previos que debes tomar en consideración antes de realizar tus cálculos.

Fuente: Pexels
Requisitos previos para hacer un cálculo de intervalo de confianza
Conocer los elementos y los objetivos de este tipo de análisis no implica que ya tienes todo lo que necesitas para hacer tus cálculos de la mejor forma posible. Debes establecer una serie de parámetros para que tu operación sea lo más fructífera posible.
¿Qué tipo de elementos debes tomar en cuenta para ello? Te recomendamos que tomes las siguientes medidas antes de realizar el cálculo del intervalo de confianza:
-
Elige el parámetro de la población de aquel lugar del que deseas obtener la estimación: por lo general, la elección de esta zona suele estar vinculada a la clase de distribución, que se asume en este caso para la variable que se busca estudiar.
-
El parámetro poblacional suele estar asociado con algunos parámetros de la distribución: a pesar de esta afirmación, en muchas ocasiones es posible que surja el interés de obtener un tipo de parámetro en concreto.
-
Otra elección que se puede trabajar es el propio nivel de confianza: aunque no lo parezca, esta variable es muy importante, ya que es la que determinará el grado de precisión de la estimación que se obtenga, relacionada con el tema del ancho del intervalo. Mientras más elevado sea el nivel de confianza exigido, más grande será el radio del intervalo, lo que también permite que la precisión en la estimación sea más reducida.
Estos son algunos requisitos que debes tomar en consideración al momento de realizar cálculos como el del intervalo de confianza. Ahora sí, ¡te presentamos cómo realizar este tipo de operaciones!
¿Cómo calcular un intervalo de confianza?
Piensa que tienes que calcular la media de una población de 3 millones de personas. ¿Imaginas tener que recolectar toda esa información para trabajar con ella? Sería una tarea de nunca acabar.
Sin embargo, ante estos casos, lo más simple sería realizar lo siguiente:
-
Establece una muestra estadística de, por ejemplo, 300 personas. Sobre esta muestra más acotada, calcula la media.
-
Una vez realizado esto, aunque seguirías sin saber el valor poblacional verdadero, piensa que este se va a situar cerca del valor muestral.
-
A esa media, súmale el margen de error y obtendrás el valor del intervalo de confianza.
-
Luego, resta la media a ese margen de error y conseguirás otro valor. Entre esos dos valores estará la media poblacional.
Básicamente, este es el procedimiento estándar para calcular el intervalo de confianza. Puede variar en función de las variables que tengas disponibles, pero, a grandes rasgos, esta es la operación que debes realizar.

Fuente: Pexels
Ejemplo del cálculo del intervalo de confianza
Para entender la fórmula de un intervalo de confianza, el sitio web Conceptos Claros, ofrece un ejemplo preciso y simple que nos permitirá entender el paso a paso.
“Imagina que coges grupos de 100 tornillos y calculas la media (el promedio) de la longitud de los tornillos de cada grupito. Es decir, creas un primer grupito de 100 tornillos y calculas su media. Luego, elabora un segundo grupito de 100 tornillos y determinas su media, y así hasta 100 o 1000 grupitos”.

Fuente: Conceptos Claros
Lo que este ejemplo quiere demostrar es que, de esa manera, conseguirás tener la media de grupos de 100 tornillos, y, al tener 100 grupos de 100 tornillos, tendrás 100 valores de medias. Así, para calcular el intervalo de confianza, construye una nueva variable con las medias de los grupos (tu variable).
En la experiencia, se puede notar que el valor central de las medias es igual al de toda una población. Sin embargo, la desviación estándar, o típica, es la desviación de la población dividida entre la raíz de números de tornillos (n) de la muestra. En este caso, hablamos de 100 tornillos.
El portal web realiza 2 aclaraciones importantes que debemos tener en cuenta:
-
La media de las medias es la media de la población.
-
La desviación estándar de las medias es la desviación estándar de la población, dividido entre la raíz del número de la muestra (Error estándar SE). Dicho de otro modo, la desviación estándar de la media, en un intervalo de confianza, es el error estándar o el error de muestreo, y depende de la cantidad de tornillos de la muestra que hayas seleccionado para calcular la media.
Interpretando un cálculo de confianza
Al momento de calcular el intervalo de confianza, cuando trabajas con muestras más pequeñas que 30, la distribución de la media tiene forma de t-student. En cambio, debido a que en este ejemplo fueron muestras de 100, el histograma de las medias será una Campana de Gauss.
En cuanto a la estimación puntual de la media, podrás realizar el cálculo con un margen de error del 95%. Con este porcentaje, tu fórmula se vería de esta manera:
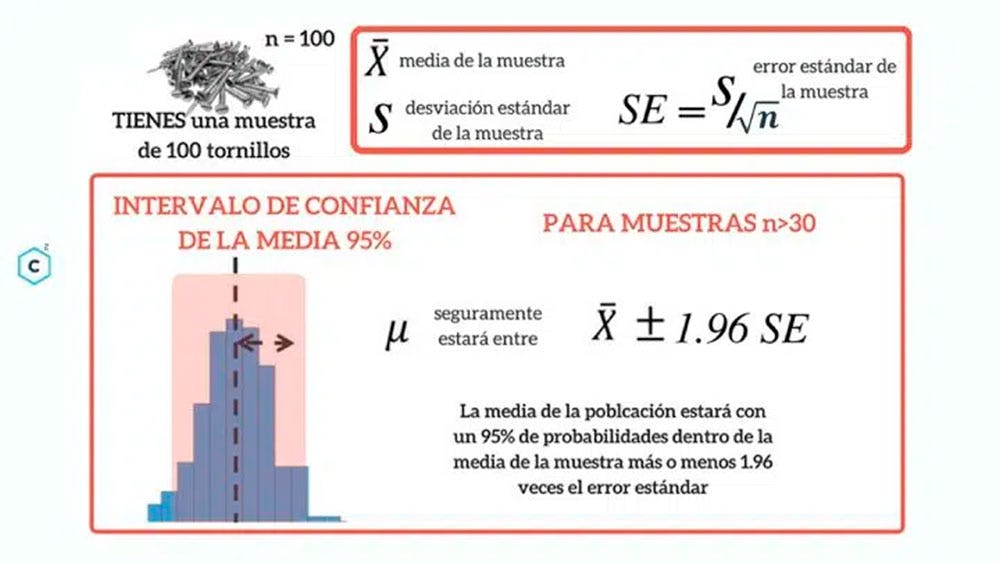
Fuente: Conceptos Claros
Así, puedes calcular la media y la desviación estándar de esa muestra, y sabrás dónde se encontrará la media de todos los tornillos con un 95% de posibilidades.
Aunque en la práctica solemos utilizar un 95%, también puedes usar el 99% para acotar un poco más tus resultados a la hora de calcular tu intervalo de confianza. Si eliges este porcentaje, trabajarás con la distribución normal estándar, el cual tiene como estimaciones puntuales de parámetros media cero y desviación estándar uno.
Ya vimos cómo trabajar con una media mayor a 30, pero, ¿qué sucede cuando el tamaño de la muestra es menor? En este caso, usarás una distribución t-student de la siguiente manera:
-
Media para muestra grandes n>= 30
IC (95%) = media +- 1.96 SE -
Media para muestras pequeñas n<30
IC(95%) = media +- t-student 0.05/2 SE
Cursos útiles para tus cálculos estadísticos
Como no podía ser de otra forma, teníamos que cerrar esta nota sobre intervalos de confianza con broche de oro. Si quieres ahondar en conceptos y elementos estadísticos, estos cursos te ayudarán a tener mucho más claros este tipo de conceptos.
¿Quieres saber más al respecto? ¡Revisa nuestras clases online!
1. Curso online de Resumiendo data y deduciendo probabilidades
Si hay un curso con el que podrás afrontar de forma práctica todo lo que involucra el intervalo de confianza, es este. Gracias a estas sesiones de clases, podrás descubrir la relevancia que tiene la estadística en los análisis de datos y la toma de decisiones de una compañía.
Durante este curso intermedio, de 1 hora y 43 minutos de duración (dividida en 24 clases), la profesora Frida Ruiz ofrece un esbozo teórico y práctico sobre cómo la estadística y el análisis y la interpretación de los datos son útiles para comprender cierto tipo de información.
Así que comenzarás a ahondar en la comprensión de los datos que se encuentren a tu alcance para que puedas entender tu información, luego de introducir variables o reducir los niveles de confianza.
En estas clases puedes aprender la conformación de las fuentes de datos y comprenderás no solo las bases estadísticas, sino también su importancia y la forma de llevar a la práctica un concepto como el de intervalo de confianza.
➤ Inscríbete a nuestro curso online de Resumiendo data y deduciendo probabilidades

2. Curso online de Matemática para el análisis de datos
Elementos como los intervalos de confianza abarcan una serie de datos que, en muchas ocasiones, resultarán fundamentales para entender un contexto particular. Lo mismo ocurre en líneas generales con las matemáticas.
Dentro del mundo del Data Science, dominar las matemáticas es imprescindible, pues ayuda en aspectos como:
-
Solución de problemas.
-
Localizar patrones.
-
Tener insights importantes en el marco de toma de decisiones.
Así que este curso será maravilloso para ti, porque enfoca las matemáticas y la estadística en torno a proyectos de investigación y situaciones cotidianas para conseguir llevarlos a cabo.
De la mano de Allan Romano, podrás comenzar a desarrollar trabajos de calidad al ser mucho más accesible para el público. Así aprenderás a abordar un análisis de datos y una investigación de probabilidades que, de la mano con el intervalo de confianza, te servirán para obtener la información necesaria para definir tus estrategias de marketing.
En este curso intermedio de 1 hora y 22 minutos de duración (divididos en 21 clases), no solo dominarás aspectos como la investigación de probabilidades, sino que también serás capaz de definir estrategias basadas en la información recabada y podrás presentar resultados complejos, como los intervalos de confianza, de maneras más simples y fáciles de explicar.
➤ Inscríbete a nuestro curso online de Matemática para el análisis de datos

3. Curso online de Interpretando datos con modelos estadísticos
Es un curso en el que la estadística pasa a llevarse a un contexto aplicado como el del machine learning. ¿En qué se relacionan ambos elementos? Te lo explicamos a continuación.
Si se desean crear soluciones de machine learning que resulten útiles para las distintas industrias, se debe dominar y entender los datos que sustentan dichas soluciones. Así que, este curso online te ofrece diversas técnicas con las cuales podrás explicar los distintos patrones que se encuentran en los sets de datos.
Analizar y entender variables (como por ejemplo las expresadas en los intervalos de confianza) te será mucho más sencillo tras estas sesiones online. De la mano de Nicolás Rodríguez aprenderás distintas metodologías para comprender datos e información estadística de manera más simple y efectiva.
Se trata de un nuevo curso de nivel intermedio (1 hora y 24 minutos de duración, segmentado en 22 clases online) en el que al final tendrás la oportunidad de diseñar tu propio modelo de machine learning con Scikit-Learn, para ser desplegado posteriormente en Google AI Platform.
➤ Inscríbete a nuestro Curso online de Interpretando datos con modelos estadísticos

Conocer elementos como el intervalo de confianza te ayudarán a interpretar de la forma adecuada algún resultado de un evento determinado. La comprensión de este concepto te será de gran utilidad para la evaluación del nivel de incidencia que puede tener una variable determinada en un contexto puntual. ¡Así que no subestimes el poder de esta variable!
Este ha sido nuestro post. Si quieres saber más acerca del intervalo de confianza, inscríbete en nuestros análisis de data, donde podrás desarrollar el análisis e interpretación de estadísticas laborales, sin importar el área de estudio (marketing, ventas, entre otras).
Además, si eres de los que prefiere tener todos los datos de su empresa ordenados y vigilados, te ofrecemos estos informes mensuales de métricas destacadas, que estamos seguros que te serán de gran utilidad para tu emprendimiento.
¡Éxitos!


